|
nømade n.14 Ottobre 2017
|
LA RIPRESA DELLE OSTILITÀ
|
7
|
|
 |
 |
 |
 |
|||||||||
|
Foglio 8
|
Foglio f.t.2 | |||||||||||
|
1.7 - Essendo solidali tra loro le due facce, la flessione del piano in G flette tutte le attualizzazioni in alfa tale che la loro condizione iniziale è al contempo condizione finale, oggetto di ogni loro propensione.
1.8 - La Generatrice è un luogo geometrico che si pone come origine di un fascio di rette che gli compete in una forma rigidamente esclusica. E' propriamente questo fascio di rette che si estende nel tempo e nello spazio a determinare il piano nelle [sue] due facce, a porsi come insieme di possibilità o condizione iniziale di ogni attualizzazione (nella fattispecie di ogni segmento) che gli si confà e che ad esso è congruente, quindi riconducibile. Egli è il sistema che ha nella generatrice, a sua volta, la propria condizione iniziale e finale, e si pone all'ermenauta come modello di competenza dell'intera fenomenologia del piano racchiudendo i valori propri a tutti i singoli fenomeni che rende possibili. 1.9 - (in definitiva) Se conoscessimo la posizione e la direzione dell'attualizzazione in un [determinato] momento protremmo predire ogni suo movimento successivo con la medesima precisione; in altre parole, la storia dinamica dell'attualizzazione e del sistema è completamente determinata dalle condizioni iniziali esprese nella propria Generatrice. 1.10 - Non si danno attualizzazioni senza sistema. Del pari, sistema senza attualizzazioni, essendo di per sé il sistema (piano senza segni) segno del sistema. 1.11 - Esistono tanti insiemi di attualizzazioni (famiglie) quanti sistemi, quante generatrici. 1.12 - Ogni attualizzazione è un segno determinato e trova in G la sua determinazione e il suo valoro, avendo in una qualche G, ma in una sola, la sua origine e ragione. 1.13 - Diverse attualizzazioni si possono raggruppare come punti di un unico sistema (come classi, famiglie) quando la somma della loro posizione, .... |
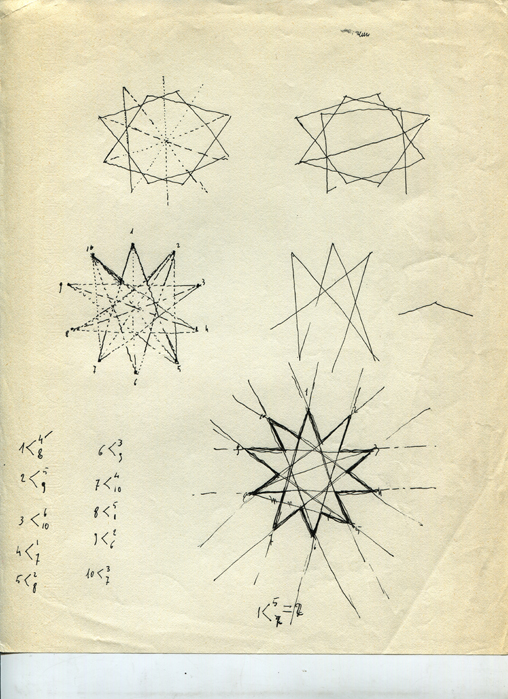
[ sopra: una generica configurazione di Generatrice delle rigature sulla faccia "gamma" del piano mentre ordina il proprio sistema fibrato sulla superficie esterna dell'universo conico) ]
|
|||||||||||
 |
|
|||||||||||
|
MENEO, O DELLA GEOMETRIA |
5
|
Carmelo L Romeo . 1970 . 2017 | ||